使用REVIVE SDK控制摆杆的运动

example-of-Pendulum-game

倒立摆杆平衡任务描述

Gym-Pendulum是传统强化学习（RL）领域中的经典控制问题之一。 如以上动画所示，摆杆的一端连接到固定点，另一端可以自由摆动。 该控制问题的目标是在摆杆的自由端施加力矩，使摆杆最终稳定地倒立于固定点之上。 在该位置，摆杆可以“站”在固定点上并保持平衡。该问题的具体说明也可以参阅 Gym-Pendulum。 在个示例中，我们试图说明如何使用REVIVE SDK构建Gym-Pendulum的虚拟环境，并基于虚拟环境学到最优的控制策略。 我们还对比REVIVE SDK输出策略和历史数据的策略表现。我们将非常直观地感受并理解REVIVE SDK的运行机制和训练效果。

Action Space

Continuous(1)

Observation

Shape (3,)

Observation

High [1. 1. 8.]

Observation

Low [-1. -1. -8.]

动作空间

对摆杆的自由端施加力矩，力矩的大小是连续分布于 [-2,2] 空间中。

观察空间

观察空间为三维，分别代表摆杆与重力方向夹角的正弦值、余弦值和此夹角的角速度值。

倒立目标

在Gym-Pendulum任务中，我们试图在摆杆的一端施加扭矩，使其倒立于固定点上。奖励函数由以下等式确定：

\[r = -(\theta^{2} + 0.1 * (d\theta/{dt})^{2} + 0.001 * {\rm torque}^2)\]

方程中，\(\theta\)rm torque` 为动作力矩。 其中方程式的最大值和最小值分别为0和-16，分别对应于摆在固定点上或倒立的摆。

import torch
import math

def get_reward(data : Dict[str, torch.Tensor]) -> torch.Tensor:
   action = data['actions'][...,0:1]
   u = torch.clamp(action, -2, 2)

   state = data['states'][...,0:3]
   costheta = state[:,0].view(-1,1)
   sintheta = state[:, 1].view(-1,1)
   thdot = state[:, 2].view(-1,1)

   x = torch.acos(costheta)
   theta = ((x + math.pi) % (2 * math.pi)) - math.pi
   costs = theta ** 2 + 0.1 * thdot**2 + 0.001 * (u**2)

   return -costs

初始状态

摆杆可以以任意夹角以及该夹角以任意速度作为摆杆的初始状态。

使用REVIVE SDK训练控制策略

REVIVE SDK是一个历史数据驱动的工具，根据文档教程部分的描述，在摆杆任务上使用REVIVE SDK可以分为以下几步：

  1. 收集任务的历史决策数据；

  2. 结合业务场景和收集的历史数据构建 决策流图和数组数据，其中决策流图主要描述了业务数据的交互逻辑， 使用 .yaml 文件进存储，数组数据存储了决策流图中定义的节点数据，使用 .npz 或 .h5 文件进行存储。

  3. 有了上述的决策流图和数组数据，REVIVE SDK已经可以进行虚拟环境模型的训练。但为了获得更优的控制策略，需要根据任务目标定义 奖励函数 ，奖励函数定义了 策略的优化目标，可以指导控制策略将摆杆倒立在固定点上。

  4. 定义完 决策流图， 训练数据 和 奖励函数 之后，我们就可以 使用REVIVE SDK开始虚拟环境模型训练和策略模型训练。

  5. 最后将REVIVE SDK训练的策略模型进行上线测试。

收集历史数据

在此示例当中，我们假设已经有了一个可以使用的摆杆控制策略（以下简称：原始策略），我们的目标是通过REVIVE训练一个比此策略更优的新策略。 我们首先使用这一原始策略来收集历史数据。

定义决策流图和准备数据

一旦有了历史决策数据，就需要根据业务场景来构建决策流程图。 决策流程图准确地定义了数据之间的决策因果关系。 在摆杆控制任务中，我们可以观察到摆杆的状态信息（ states ）。 状态是一个三维量，分别代表摆杆与重力方向夹角的正弦值、余弦值和此夹角的角速度。 控制策略 actions 根据 states 的信息来对摆杆的自由端施加力矩。

下面的示例显示 .yaml 中的详细信息。通常，有两部分信息构成 .yaml 文件，分别是 graph 和 columns 。 其中 graph 部分定义了决策流图。 columns 部分定义了数据的组成。 具体请参考文档：准备数据 。 请注意，由于 states 存在三个维度， states 的列应该按顺序定义在 columns 部分。 如 gym-pendulum 所示， 状态和动作中的变量是连续分布的，我们使用 continuous 来描述每一列数据。

metadata:

   graph:             <- 'graph'部分
     actions:         <- 对应于 '.npz' 的 `actions`.
       - states       <- 对应于 '.npz' 的 `states`.
     next_states:
       - states       <- 对应于 '.npz' 的 `states`.
       - actions      <- 对应于 '.npz' 的 `actions`.

   columns:           <- 'columns'部分
     - obs_0:               ---+
       dim: states             |
       type: continuous        |
     - obs_1:                  |    这里, 'dim:states' 对应 '.npz' 的 'states'
       dim: states             | <- 'obs_*' 表示第*维的 'states'。
       type: continuous        |
     - obs_2                   |    因为'states'有三个维度，我们按照维度的顺序在
       dim: states             |    'columns'中进行了定义
       type: continuous     ---+
     - action:
       dim: actions
       type: continuous

根据 准备数据 将数据转换为 .npz 文件进行存储 。

定义奖励函数

奖励函数的设计对于学习策略至关重要。一个好的奖励函数应该能够指导策略向着预期的方向进行学习。REVIVE SDK支持支持以python源文件的方式定义奖励函数。

倒立摆杆的目标在于将摆杆倒立在固定点上，此时与重力的反方向夹角为0度，并获得最高奖励值0。 当摆杆垂直悬挂在固定点上时，此时夹角为最大值180度，获得最小的奖励-16.

\[r = -(\theta^{2} + 0.1 * (d\theta/{dt})^{2} + 0.001 * {\rm torque}^2)\]

其中方程式的最大值和最小值分别为0和-16，分别对应于摆在固定点上或倒立的摆。

import torch
import math

def get_reward(data : Dict[str, torch.Tensor]) -> torch.Tensor:
   action = data['actions'][...,0:1]
   u = torch.clamp(action, -2, 2)

   state = data['states'][...,0:3]
   costheta = state[:,0].view(-1,1)
   sintheta = state[:, 1].view(-1,1)
   thdot = state[:, 2].view(-1,1)

   x = torch.acos(costheta)
   theta = ((x + math.pi) % (2 * math.pi)) - math.pi
   costs = theta ** 2 + 0.1 * thdot**2 + 0.001 * (u**2)

   return -costs

定义奖励函数的更多细节描述可以参考 准备数据 章节的文档介绍。

使用REVIVE SDK训练控制策略

我们已经构建完成运行REVIVE SDK所需的文件，包括 .npz 数据文件、 .yaml 文件和 reward.py 奖励函数。 这三个文件位于 data 文件夹中。其中还有另一个文件 config.json， 该文件保存了训练所需的超参数。

我们可以使用下面的命令开启模型训练：

python train.py -df data/expert_data.npz -cf data/Env-GAIL-pendulum.yaml -rf data/pendulum-reward.py -rcf data/config.json -vm once -pm once --run_id pendulum-v1 --revive_epoch 1000 --ppo_epoch 5000 --venv_rollout_horizon 50 --ppo_rollout_horizon 50

训练模型的更多细节描述可以参考 准备数据 章节的文档介绍。

Note

REVIVE SDK已提供运行示例所需数据和代码，支持一键运行。数据和代码存储在 SDK源码库。

在任务场景中测试策略模型来控制Gym-Pendulum任务

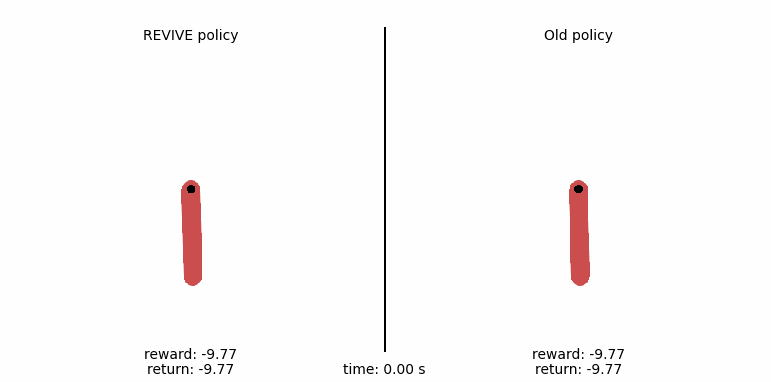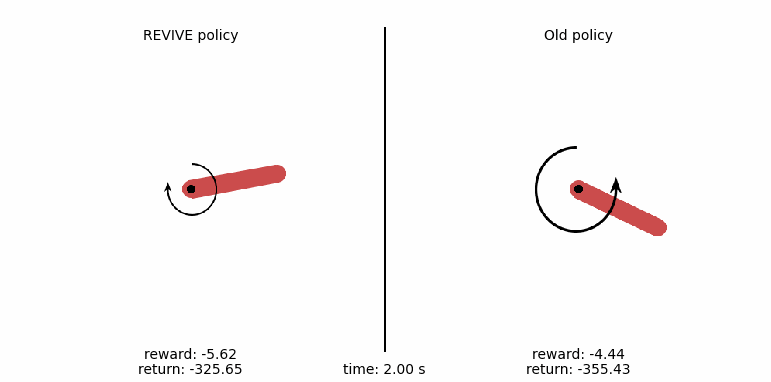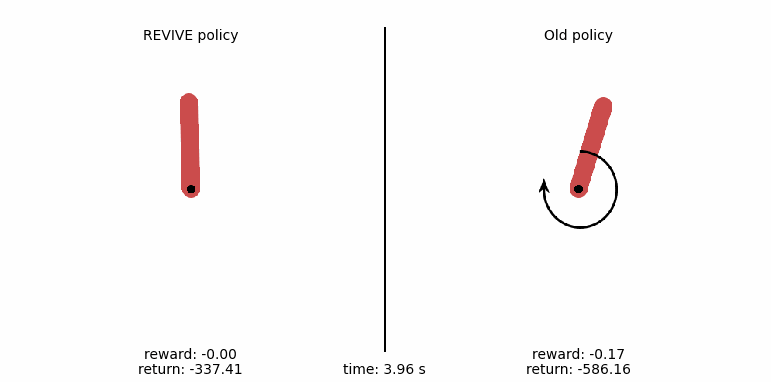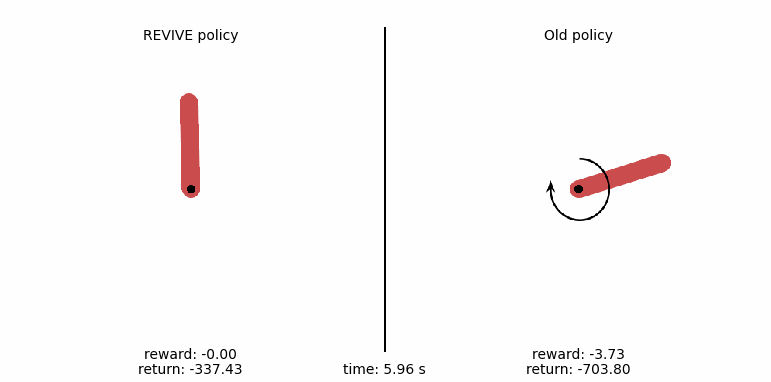
最后，我们从日志文件中获得了REVIVE SDK训练后的控制策略，该策略保存路径为 logs\pendulum-v1\policy.pkl 。 我们尝试在Gym-Pendulum环境上测试策略的效果，并和历史数据中的控制策略（原始策略）进行对比。在下面的测试代码中， 我们将策略在Gym-Pendulum环境中随机测试50次，每次执行300个时间步长，最后输出这50次的平均回报（累计奖励）。 REVIVE SDK的策略获得了-137.66平均奖励，远高于数据中原始策略的-861.74奖励值，控制效果提高了约84%。

import warnings
warnings.filterwarnings('ignore')

from Results import get_results
import pickle

result = get_results('logs/pendulum-v1/policy.pkl', 'url/Old_policy.pkl')
r_revive, r_old, vedio_revive, vedio_old = result.roll_out(50, step=300)

with open('url/results.pkl', 'wb') as f:
pickle.dump([vedio_revive, vedio_old], f)

# 输出:
# REVIVE平均回报: -137.66
#    原始平均回报: -861.74

为了更直观地比较策略，我们通过下面的代码生成策略的控制动画。我们在动画中展示钟摆运动的每一步， 从比较来看，左侧由REVIVE SDK输出的策略摆可以在3秒内将摆杆稳定地倒立在平衡点上， 而右侧数据中的原始策略始终不能将摆控制到目标位置。

from Video import get_video
from IPython import display
%matplotlib notebook

vedio_revive, vedio_old = pickle.load(open('url/results.pkl', 'rb'))
html = get_video(vedio_revive,vedio_old)
display.display(html)
example-of-Pendulum-game